How to program a hexagonal grid

I decided to try and program a hexagonal grid using Java. This will be the basis for future hexagon based games (Civilization, Hive). As always, I’m going to try to make this program as general as possible.
I found some useful websites to get started with (I wouldn’t have known where to start otherwise). Some of the images below are from these pages. However, none of these websites is complete and a couple have errors, thus I am writing this instruction page.
http://www.codeproject.com/Articles/14948/Hexagonal-grid-for-games-and-other-projects-Part-1
http://weblogs.java.net/blog/malenkov/archive/2009/02/hexagonal_tile.html
http://www.tonypa.pri.ee/tbw/tut25.html

1. There are two possible orientations for hexagons (a.k.a. hexes): flat and pointy.
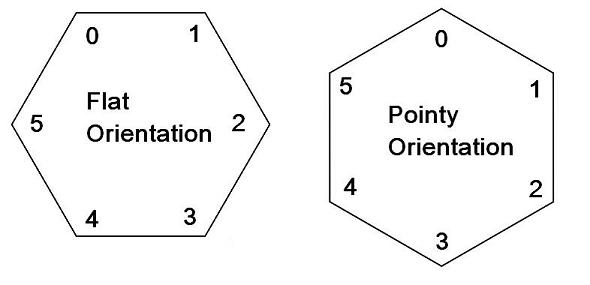
Flat and Pointy Hexagons
Flat orientation makes vertical columns of hexagons, while pointy orientation makes horizontal rows:
   
We’re only going to be using the FLAT orientation. The program would have to be rewritten to handle the math for the pointy orientation.

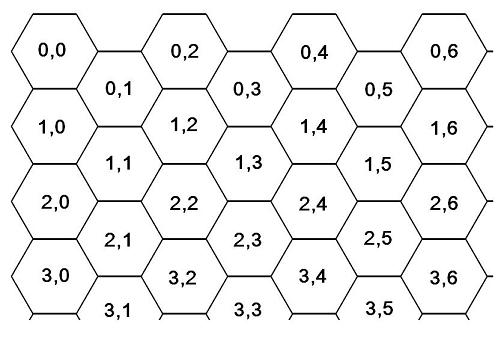
2. Hexes are numbered as follows:
two dimensional hexagon array
3. Defining measurements for the hexagons:

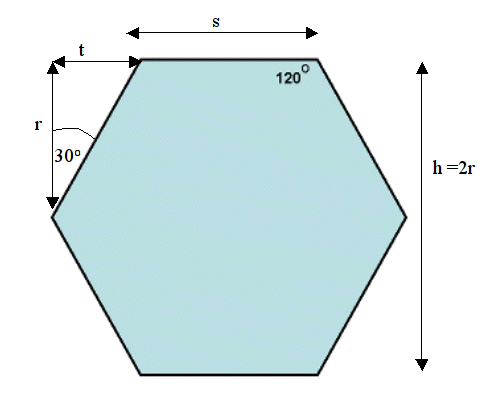
The size of the hexagon will be in pixels and can be specified using either height (h) or sidelength (s). No matter which way we are measuring the hexagon, we will have to calculate all 4 variables: h, r, s, t.
I’m using the letter ‘t’ because there is already an ‘r’ and an ‘s’.  Note that we never really need the width (w = s + 2t). I probably should have used something other than “h” for the height, because the other variables work when the hexagon is rotated to be pointy.
FYI: here is a set of dimensions for a Pointy orientation.
(Again “h” is a weird dimension. I do like the usage of “a” and “b” though.)
4. We need to decide on the location of (0,0) in each hexagon.
There are two possibilities indicated by yellow fuzzies:

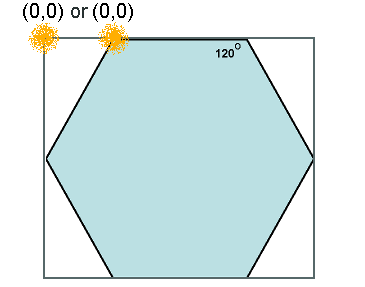
The boolean variable “XYVertex” will be used to indicate the choice.
The leftmost option (XYVertex = false) is preferable I think, although making (0,0) as the first vertex on the hexagon (XYVertex = true) also works fine.
5. Converting a mouse click to a hexagon co-ordinate.
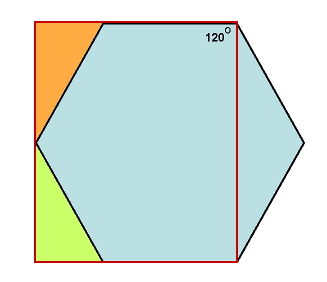
This is the tricky part that I wasn’t able to get from the internet. The simplest method is to detect clicks in the red rectangles in the image below. Initially treating the board as a rectangular grid works fine. The odd numbered columns must have h/2 added to their y value because they are lower than the even numbered columns. This is shown in column #3.

The coordinates of hexagon A are (2,1). We need to ensure that any click inside hexagon A returns this value.

  1. Detect if the mouse is clicked in the red rectangle.
  2. Calculate the row and column of the rectangle.
  3. Determine if the mouse was clicked in the orange triangle. If so, change the coordinates to be the hex above and to the left.
  4. Determine if the mouse was clicked in the green triangle. If so, change the coordinates to be for the hex below and to the left.
  5. The right most part of the hex — the blue part outside the red square — will be handled by the same algorithm but for the hexes that are in the next column over.
  6. Note that changing the coordinates for clicking in the two coloured triangles will be different depending on whether the hexagon is in an even or odd column

Finally, here’s the complete code (hosted on GitHub).

There are two java files: hexgame.java and hexmech.java (locally hosted).  The first one has the code for the graphics and the main part of whatever game is played. The second file has the mechanics for calculating anything to do with the hexagons. It also paints the hexagons based on the contents of a board array. (As I improve the inline documentation, I’ll upload new versions of the files.)

Steps I followed to do a program like this:

  1. draw a line on a JPanel
  2. learn how to make a polygon for a hexagon.
  3. use drawPolygon() to display a hexagon on the screen (the JPanel).
  4. use variables to set the hexagon size, calculate h,r,s,t
  5. make a grid of hexagons on the screen
  6. colour in hexagons based on the contents of an array representing the board
  7. add in borders to offset the hexagons from the edge of the screen
  8. detect mouse clicks
  9. convert mouse clicks to correct hex co-ordinates.

 Here is the final result: